Wheatstone Bridges

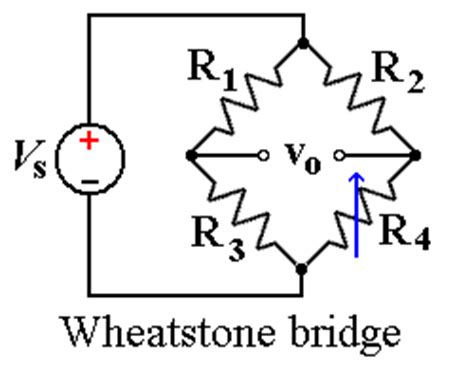
Introduction to the Wheatstone Bridge

The Wheatstone Bridge is a fundamental electrical circuit used for measuring an unknown resistance with high precision. It was invented by Samuel Hunter Christie in 1833 and improved and popularized by Sir Charles Wheatstone in 1843. The bridge consists of four resistors arranged in a diamond-shaped configuration, with a voltage source connected across one diagonal and a voltage measuring device (galvanometer) connected across the other diagonal.

The Basic Principle of the Wheatstone Bridge

The principle behind the Wheatstone Bridge is based on the concept of a balanced bridge. When the bridge is balanced, the voltage difference between the two midpoints of the bridge (where the galvanometer is connected) is zero. This balanced condition occurs when the ratio of the resistances in the two arms of the bridge is equal.

Mathematically, the balance condition can be expressed as:

R1 / R2 = R3 / Rx

Where:
– R1 and R3 are known resistances
– R2 is an adjustable resistance (usually a potentiometer)
– Rx is the unknown resistance to be measured

Wheatstone Bridge Circuit Analysis

Kirchhoff’s Laws and the Wheatstone Bridge

To understand the operation of the Wheatstone Bridge, we need to apply Kirchhoff’s Laws:

1. Kirchhoff’s Current Law (KCL): The sum of currents entering a node is equal to the sum of currents leaving the node.
2. Kirchhoff’s Voltage Law (KVL): The sum of all voltages around a closed loop is equal to zero.

By applying these laws to the Wheatstone Bridge circuit, we can derive the balance condition equation.

Derivation of the Balance Condition Equation

Let’s assume that the bridge is balanced, and the current through the galvanometer is zero. We can then apply KVL to the two loops of the bridge:

Loop 1 (left side):

V - I1 * R1 - I2 * R2 = 0

Loop 2 (right side):

V - I1 * R3 - I2 * Rx = 0

Since the current through the galvanometer is zero, we can say that:

I1 * R1 = I2 * R2
I1 * R3 = I2 * Rx

Dividing these two equations, we get:

(I1 * R1) / (I2 * R2) = (I1 * R3) / (I2 * Rx)

Simplifying this equation yields the balance condition:

R1 / R2 = R3 / Rx

Types of Wheatstone Bridges

There are several variations of the Wheatstone Bridge, each designed for specific applications or to overcome certain limitations. Some of the most common types include:

DC Wheatstone Bridge

The DC Wheatstone Bridge is the most basic form of the bridge, using DC voltage sources and resistors. It is suitable for measuring static resistances and is widely used in laboratory settings.

AC Wheatstone Bridge

The AC Wheatstone Bridge uses an AC voltage source instead of a DC source. This allows for the measurement of impedance (resistance, capacitance, and inductance) rather than just resistance. AC bridges are used in applications such as measuring the impedance of transducers, sensors, and other components.

Kelvin Double Bridge

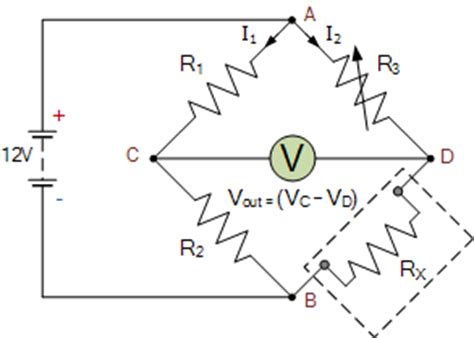
The Kelvin Double Bridge is an extension of the basic Wheatstone Bridge, designed to minimize the effect of lead and contact resistances when measuring low resistances (typically less than 1 ohm). It uses four terminal connections to the unknown resistance, effectively separating the current-carrying and voltage-sensing paths.

Murray Loop Bridge

The Murray Loop Bridge is a variation of the Wheatstone Bridge used for locating faults in electrical cables. It consists of a single loop of wire with the bridge connected at one end and the fault at an unknown location along the loop. By balancing the bridge, the distance to the fault can be determined.

Applications of Wheatstone Bridges

Wheatstone Bridges find applications in various fields, ranging from electrical engineering to biomedical instrumentation. Some common applications include:

Strain Gauge Measurement

Strain gauges are resistive sensors that change resistance when subjected to mechanical strain. They are often used in a Wheatstone Bridge configuration to measure force, pressure, or displacement. The bridge helps to convert the small resistance changes into measurable voltage signals.

Temperature Measurement

Resistance Temperature Detectors (RTDs) and thermistors are temperature-sensitive resistors that can be used in a Wheatstone Bridge to measure temperature. The bridge helps to linearize the output and provides a voltage signal proportional to the temperature change.

Load Cell Measurement

Load cells are force sensors that use strain gauges to measure weight or force. They are commonly used in a Wheatstone Bridge configuration to provide accurate and stable measurements in applications such as weighing scales, force sensors, and pressure transducers.

Biomedical Instrumentation

Wheatstone Bridges are used in various biomedical instruments to measure physiological parameters. For example:

• Blood pressure measurement: Strain gauge-based pressure sensors in a Wheatstone Bridge configuration are used to measure blood pressure in invasive and non-invasive blood pressure monitors.
• Respiratory monitoring: Wheatstone Bridges with resistive sensors are used to measure respiratory parameters such as airflow, lung volume, and chest wall movement.
• Bioimpedance measurement: AC Wheatstone Bridges are used to measure the electrical impedance of biological tissues, which can provide information about body composition, fluid status, and cellular health.

Advantages and Limitations of Wheatstone Bridges

Advantages

1. High accuracy: Wheatstone Bridges provide highly accurate resistance measurements, making them suitable for precise measurement applications.
2. Sensitivity: The bridge configuration allows for the detection of small changes in resistance, enabling the measurement of small signals.
3. Temperature compensation: By using matched resistors or temperature-compensated resistors, the effect of temperature variations on the measurement can be minimized.
4. Versatility: Wheatstone Bridges can be used with various types of resistive sensors, making them adaptable to a wide range of applications.

Limitations

1. Limited frequency range: Basic DC Wheatstone Bridges are not suitable for measuring resistances at high frequencies due to the effects of stray capacitance and inductance.
2. Nonlinearity: If the resistive sensor has a nonlinear response, the output of the Wheatstone Bridge will also be nonlinear, requiring additional linearization techniques.
3. Sensitivity to lead resistance: In some cases, the resistance of the connecting leads can introduce errors in the measurement, especially when measuring low resistances.
4. Requires manual balancing: Traditional Wheatstone Bridges require manual adjustment of the variable resistor to achieve balance, which can be time-consuming and prone to human error.

Modern Developments and Innovations

Despite its limitations, the Wheatstone Bridge remains a fundamental tool for resistance measurement. However, modern innovations have led to improved versions of the bridge and alternative techniques for resistance measurement:

Automated Wheatstone Bridges

Automated Wheatstone Bridges use electronic circuits and microcontrollers to automatically balance the bridge and provide a digital output. This eliminates the need for manual balancing and improves the speed and accuracy of measurements.

Digital Resistance Measurement Techniques

With the advent of high-resolution analog-to-digital converters (ADCs) and digital signal processing (DSP) techniques, alternative methods for resistance measurement have emerged. These include:

• Ratiometric resistance measurement: This technique uses a known reference resistance and measures the ratio of the unknown resistance to the reference using ADCs.
• Current-to-voltage conversion: By passing a known current through the unknown resistance and measuring the resulting voltage drop, the resistance can be calculated using Ohm’s Law.

Integrated Circuit-Based Solutions

Integrated circuits (ICs) specifically designed for resistance measurement have been developed, offering compact and cost-effective solutions. These ICs often include built-in excitation sources, amplifiers, ADCs, and digital interfaces, simplifying the design of resistance measurement systems.

FAQ

Q1: What is a Wheatstone Bridge?

A: A Wheatstone Bridge is an electrical circuit used for measuring an unknown resistance by balancing two legs of a bridge circuit, one containing the unknown component.

Q2: How does a Wheatstone Bridge work?

A: A Wheatstone Bridge works by comparing the unknown resistance to known resistances in a balanced bridge configuration. When the bridge is balanced, the voltage difference between the midpoints of the bridge is zero, indicating that the ratio of resistances in the two arms is equal.

Q3: What are the main applications of Wheatstone Bridges?

A: Wheatstone Bridges are used in various applications, including strain gauge measurement, temperature measurement, load cell measurement, and biomedical instrumentation.

Q4: What are the advantages of using a Wheatstone Bridge?

A: The main advantages of using a Wheatstone Bridge are high accuracy, sensitivity to small resistance changes, temperature compensation, and versatility in adapting to different types of resistive sensors.

Q5: Are there any limitations to using Wheatstone Bridges?

A: Yes, Wheatstone Bridges have some limitations, such as a limited frequency range, nonlinearity when using nonlinear sensors, sensitivity to lead resistance, and the need for manual balancing in traditional bridges. However, modern developments and innovations have addressed some of these limitations.

Conclusion

The Wheatstone Bridge has been a cornerstone of resistance measurement for over a century, providing a simple yet powerful tool for accurate and sensitive measurements. Its principle of operation, based on the balance of resistances in a bridge configuration, has found applications in various fields, from electrical engineering to biomedical instrumentation.

Despite its limitations, the Wheatstone Bridge remains relevant in modern measurement systems, with ongoing developments and innovations aimed at improving its performance and usability. As technology advances, we can expect to see further refinements and adaptations of the Wheatstone Bridge, ensuring its continued importance in the world of precise resistance measurement.