Introduction to Skin Effect
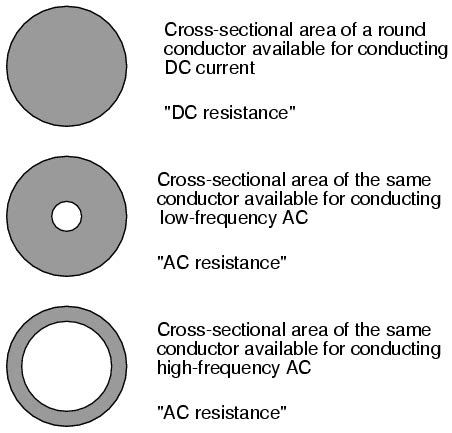
The skin effect is a phenomenon observed in alternating current (AC) systems where the current density is highest near the surface of a conductor and decreases exponentially with depth. This effect arises due to the interaction between the electromagnetic fields and the conductor, leading to a non-uniform distribution of current within the conductor. The skin effect has significant implications for the design and performance of electrical systems, particularly at high frequencies.
Causes of Skin Effect
The skin effect is caused by two primary factors:
- Electromagnetic Induction: When an alternating current flows through a conductor, it generates a time-varying magnetic field around the conductor. This magnetic field, in turn, induces eddy currents within the conductor itself. These eddy currents flow in loops perpendicular to the direction of the main current and oppose the flow of current in the center of the conductor.
- Self-Inductance: The eddy currents induced by the magnetic field also contribute to the self-inductance of the conductor. Self-inductance is the property of a conductor that opposes changes in the current flowing through it. As the frequency of the alternating current increases, the self-inductance becomes more significant, further concentrating the current towards the surface of the conductor.
Skin Depth
The skin depth is a measure of how deeply the current penetrates into a conductor at a given frequency. It is defined as the depth at which the current density has decreased to 1/e (approximately 0.368) of its value at the surface. The skin depth is denoted by the Greek letter delta (δ) and is given by the following formula:
δ = sqrt(2 / (ω * μ * σ))
Where:
– ω is the angular frequency of the current (ω = 2π * frequency)
– μ is the magnetic permeability of the conductor material
– σ is the electrical conductivity of the conductor material
As the frequency of the current increases, the skin depth decreases, resulting in a thinner layer of current flow near the surface of the conductor.
Current Density Distribution
The current density distribution within a conductor is not uniform when the skin effect is present. The current density is highest at the surface and decreases exponentially with depth. This non-uniform distribution can be described mathematically using the following equation:
J(x) = J_s * e^(-x/δ)
Where:
– J(x) is the current density at a depth x from the surface
– J_s is the current density at the surface
– δ is the skin depth
The exponential decay of the current density with depth is a key characteristic of the skin effect. The table below illustrates how the current density decreases relative to the depth in terms of the skin depth:
| Depth (x) | Current Density (J(x)) |
|---|---|
| 0 | J_s |
| δ | 0.368 * J_s |
| 2δ | 0.135 * J_s |
| 3δ | 0.050 * J_s |
| 4δ | 0.018 * J_s |
| 5δ | 0.007 * J_s |
As evident from the table, the current density rapidly decreases as the depth increases, with the majority of the current flowing within the first few skin depths.
Resistance and Power Loss
The skin effect has a direct impact on the resistance and power loss of a conductor. Due to the non-uniform current distribution, the effective cross-sectional area of the conductor is reduced, leading to an increase in resistance. The AC resistance of a conductor with skin effect can be approximated using the following formula:
R_ac = R_dc * (1 + (f/f_c)^2)
Where:
– R_ac is the AC resistance
– R_dc is the DC resistance
– f is the frequency of the current
– f_c is the critical frequency at which the skin depth equals the conductor radius
As the frequency increases, the AC resistance of the conductor also increases, resulting in higher power losses. The power loss due to the skin effect can be calculated using the following equation:
P_loss = I^2 * R_ac
Where:
– P_loss is the power loss
– I is the RMS value of the current
– R_ac is the AC resistance
The increased power loss due to the skin effect can lead to reduced efficiency and potential overheating of the conductor, especially at high frequencies.

Electromagnetic Field Distribution
The skin effect not only affects the current density distribution but also influences the electromagnetic field distribution around the conductor. The time-varying current in the conductor generates a time-varying magnetic field, which in turn induces an electric field. The distribution of these fields is closely related to the current density distribution.
Magnetic Field
The magnetic field generated by the current in a conductor with skin effect is strongest near the surface and decays exponentially with distance from the surface. The magnetic field intensity at a distance r from the center of the conductor can be described by the following equation:
H(r) = (I / (2πr)) * (1 – e^(-r/δ))
Where:
– H(r) is the magnetic field intensity at a distance r
– I is the total current flowing through the conductor
– δ is the skin depth
The magnetic field lines circulate around the conductor in concentric circles, with the field strength being highest near the surface and decreasing rapidly with distance.
Electric Field
The time-varying magnetic field generated by the current also induces an electric field within the conductor. The electric field is responsible for the flow of eddy currents and is perpendicular to both the magnetic field and the direction of the main current. The electric field intensity at a depth x from the surface can be expressed as:
E(x) = ω * μ * H_s * e^(-x/δ)
Where:
– E(x) is the electric field intensity at a depth x
– ω is the angular frequency of the current
– μ is the magnetic permeability of the conductor material
– H_s is the magnetic field intensity at the surface
– δ is the skin depth
The electric field is strongest at the surface and decays exponentially with depth, similar to the current density distribution.

Implications and Applications
The skin effect has several important implications and applications in various fields of electrical engineering:
High-Frequency Systems
The skin effect is particularly significant in high-frequency systems, such as radio frequency (RF) and microwave circuits. At these frequencies, the skin depth becomes very small, and the current is confined to a thin layer near the surface of the conductor. This can lead to increased losses and reduced efficiency. To mitigate the effects of skin effect, designers often use specialized conductors, such as litz wire or hollow conductors, which have a larger surface area to volume ratio.
Power Transmission
In power transmission systems, the skin effect can cause additional power losses and reduce the effective current-carrying capacity of the conductors. To minimize these losses, power transmission lines often use stranded conductors or bundled conductors, which have a larger surface area compared to solid conductors of the same cross-sectional area. Additionally, the use of higher voltage levels helps to reduce the current and, consequently, the skin effect losses.
Shielding and EMC
The skin effect is also exploited in the design of electromagnetic shielding and electromagnetic compatibility (EMC) solutions. Conductive enclosures and shielding materials rely on the skin effect to attenuate electromagnetic fields and prevent interference. By choosing materials with high conductivity and appropriate thickness, designers can effectively shield sensitive electronic components from external electromagnetic disturbances.
Induction Heating
Induction heating is another application that leverages the skin effect. In induction heating, a high-frequency alternating current is passed through a coil, generating a strong magnetic field. When a conductive material is placed within this field, eddy currents are induced on the surface of the material, causing it to heat up. The skin effect concentrates the induced currents near the surface, resulting in efficient and localized heating of the material.
Frequently Asked Questions (FAQ)
- What is the skin effect?
The skin effect is a phenomenon in which the current density in a conductor is highest near the surface and decreases exponentially with depth when carrying alternating current. - What causes the skin effect?
The skin effect is caused by electromagnetic induction and self-inductance. The time-varying magnetic field generated by the alternating current induces eddy currents within the conductor, which oppose the flow of current in the center and concentrate the current towards the surface. - How does the frequency of the current affect the skin effect?
As the frequency of the alternating current increases, the skin depth decreases, resulting in a thinner layer of current flow near the surface of the conductor. Higher frequencies lead to more pronounced skin effect and increased AC resistance. - What is the skin depth?
The skin depth is a measure of how deeply the current penetrates into a conductor at a given frequency. It is defined as the depth at which the current density has decreased to 1/e (approximately 0.368) of its value at the surface. - How can the skin effect be mitigated in practical applications?
To mitigate the effects of skin effect, designers can use specialized conductors with a larger surface area to volume ratio, such as litz wire or hollow conductors. In power transmission systems, stranded or bundled conductors and higher voltage levels are used to reduce skin effect losses. Proper material selection and thickness are also important for effective shielding and EMC solutions.
Conclusion
The skin effect is a fundamental phenomenon in alternating current systems that arises due to the interaction between electromagnetic fields and conductors. It results in a non-uniform distribution of current density, with the current being concentrated near the surface of the conductor. The skin effect has significant implications for the resistance, power loss, and electromagnetic field distribution in electrical systems.
Understanding the skin effect is crucial for the design and optimization of high-frequency systems, power transmission lines, electromagnetic shielding, and induction heating applications. By considering the skin depth, material properties, and frequency of operation, engineers can mitigate the adverse effects of skin effect and improve the efficiency and performance of electrical systems.
As technology continues to advance and the demand for high-frequency applications grows, the study of skin effect remains an essential area of research and development. Further advancements in materials science, computational modeling, and manufacturing techniques will enable the development of more efficient and reliable electrical systems that can effectively manage the challenges posed by the skin effect.

No responses yet