kramer kronigs relationship pcbs

Introduction to Kramers-Kronig Relations and PCBs

The Kramers-Kronig relations are a set of mathematical equations that describe the relationship between the real and imaginary parts of a complex function. These relations have found widespread applications in various fields of physics and engineering, including the analysis of printed circuit boards (PCBs). PCBs are essential components in modern electronics, providing a platform for interconnecting electronic components and enabling the functioning of complex electronic systems.

In this article, we will delve into the Kramers-Kronig relations and their relevance to PCBs. We will explore the fundamental concepts behind these relations, their mathematical formulation, and their practical implications in the design and analysis of PCBs. Additionally, we will discuss the challenges and limitations associated with applying Kramers-Kronig relations to PCBs and highlight some recent advancements in this field.

Understanding the Kramers-Kronig Relations

The Kramers-Kronig relations are named after the physicists Hendrik Anthony Kramers and Ralph de Laer Kronig, who independently derived these relations in the 1920s. The relations establish a connection between the real and imaginary parts of a complex function, such as the dielectric constant or the refractive index of a material.

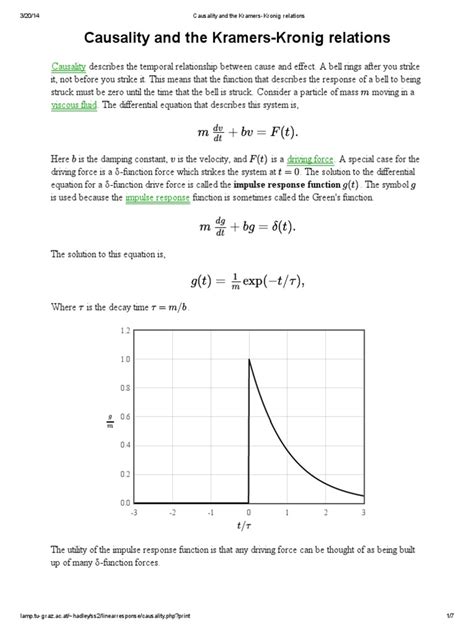
The Kramers-Kronig relations are based on the principle of causality, which states that the response of a system cannot precede the stimulus that caused it. In other words, the effect cannot occur before the cause. This principle imposes certain constraints on the behavior of physical systems and leads to the Kramers-Kronig relations.

The general form of the Kramers-Kronig relations can be expressed as follows:

Re[f(ω)] = (1/π) P ∫₋∞^∞ (Im[f(ω')] / (ω' - ω)) dω'
Im[f(ω)] = -(1/π) P ∫₋∞^∞ (Re[f(ω')] / (ω' - ω)) dω'

Here, f(ω) is a complex function of the angular frequency ω, Re[f(ω)] and Im[f(ω)] represent the real and imaginary parts of f(ω), respectively, and P denotes the Cauchy principal value of the integral.

These relations imply that if we know the real part of a complex function over the entire frequency range, we can calculate the imaginary part, and vice versa. This property has significant implications in various fields, including the analysis of PCBs.

Request PCB Manufacturing & Assembly Quote Now

Kramers-Kronig Relations in PCB Analysis

PCBs are complex structures that consist of conductive traces, dielectric materials, and various components. The electrical behavior of PCBs is governed by the properties of these materials, including their dielectric constant and conductivity. The Kramers-Kronig relations provide a powerful tool for analyzing the frequency-dependent behavior of PCBs and extracting valuable information about their electrical characteristics.

Dielectric Constant and Loss Tangent

One of the key applications of Kramers-Kronig relations in PCB analysis is the determination of the dielectric constant and loss tangent of the materials used in the PCB. The dielectric constant, denoted as εᵣ, is a measure of a material’s ability to store electrical energy, while the loss tangent, denoted as tan δ, quantifies the dissipation of electrical energy in the material.

The Kramers-Kronig relations allow us to calculate the real and imaginary parts of the dielectric constant from measured or simulated data. The real part of the dielectric constant, εᵣ', represents the energy storage capability of the material, while the imaginary part, εᵣ'', is related to the dielectric loss.

Using the Kramers-Kronig relations, we can express the real and imaginary parts of the dielectric constant as follows:

εᵣ'(ω) = 1 + (2/π) P ∫₀^∞ (ω' εᵣ''(ω') / (ω'² - ω²)) dω'
εᵣ''(ω) = -(2ω/π) P ∫₀^∞ (εᵣ'(ω') - 1) / (ω'² - ω²)) dω'

By measuring the dielectric constant over a range of frequencies and applying these relations, we can obtain a complete characterization of the material’s dielectric properties.

Transmission Line Parameters

Another important application of Kramers-Kronig relations in PCB analysis is the determination of transmission line parameters. Transmission lines are the interconnects used to transmit high-frequency signals between components on a PCB. The behavior of transmission lines is characterized by their characteristic impedance, propagation constant, and attenuation constant.

The Kramers-Kronig relations can be used to calculate these parameters from the measured or simulated scattering parameters (S-parameters) of the transmission line. The S-parameters describe the reflection and transmission of signals at the ports of a network, such as a transmission line.

Using the Kramers-Kronig relations, we can express the characteristic impedance Z₀ and the propagation constant γ of a transmission line as follows:

Z₀(ω) = (R(ω) + jωL(ω)) / (G(ω) + jωC(ω))
γ(ω) = √((R(ω) + jωL(ω))(G(ω) + jωC(ω)))

Here, R, L, G, and C represent the frequency-dependent resistance, inductance, conductance, and capacitance per unit length of the transmission line, respectively.

By applying the Kramers-Kronig relations to the measured or simulated S-parameters, we can extract the transmission line parameters and gain insights into the signal integrity and power integrity of the PCB.

Challenges and Limitations

While the Kramers-Kronig relations provide a powerful tool for analyzing PCBs, there are several challenges and limitations associated with their application in practice.

Measurement Limitations

One of the main challenges in applying Kramers-Kronig relations to PCBs is the accuracy and bandwidth of the measurement techniques. The relations require data over a wide frequency range, often extending from DC to high frequencies. However, measuring the dielectric properties or S-parameters of PCBs over such a wide frequency range can be challenging due to the limitations of the measurement equipment and the presence of noise and artifacts.

To overcome these limitations, various techniques have been developed, such as time-domain reflectometry (TDR), vector network analyzer (VNA) measurements, and broadband dielectric spectroscopy. These techniques aim to provide accurate and reliable data over a wide frequency range, enabling the application of Kramers-Kronig relations.

Numerical Challenges

Another challenge in applying Kramers-Kronig relations to PCBs is the numerical computation of the integrals involved in the relations. The integrals extend over an infinite frequency range and may contain singularities or poles, making their numerical evaluation challenging.

To address these challenges, various numerical techniques have been developed, such as the use of adaptive quadrature methods, contour integration, and analytic continuation. These techniques aim to provide accurate and efficient numerical evaluation of the Kramers-Kronig integrals, enabling their practical application in PCB analysis.

Material Nonlinearities

The Kramers-Kronig relations are based on the assumption of linear and time-invariant systems. However, PCBs often contain nonlinear materials, such as ferroelectric or ferromagnetic substances, which exhibit nonlinear behavior. The presence of nonlinearities can introduce additional complexities in the application of Kramers-Kronig relations.

To handle material nonlinearities, extensions of the Kramers-Kronig relations have been developed, such as the nonlinear Kramers-Kronig relations. These extended relations take into account the nonlinear behavior of materials and provide a framework for analyzing PCBs with nonlinear components.

Recent Advancements and Future Directions

Despite the challenges and limitations, the application of Kramers-Kronig relations to PCBs has seen significant advancements in recent years. Researchers and engineers have been working on developing new techniques and methodologies to improve the accuracy, efficiency, and practicality of Kramers-Kronig-based PCB analysis.

Some of the recent advancements include:

Broadband Dielectric Spectroscopy: The development of advanced dielectric spectroscopy techniques, such as time-domain spectroscopy and frequency-domain spectroscopy, has enabled the measurement of dielectric properties over a wide frequency range. These techniques provide accurate and reliable data for the application of Kramers-Kronig relations.
Computational Electromagnetics: The integration of Kramers-Kronig relations with computational electromagnetics methods, such as the finite-difference time-domain (FDTD) method and the method of moments (MoM), has enabled the simulation and analysis of complex PCB structures. These combined approaches provide a powerful tool for predicting the electrical behavior of PCBs and optimizing their design.
Machine Learning and Data-Driven Approaches: The application of machine learning techniques, such as artificial neural networks and support vector machines, to Kramers-Kronig-based PCB analysis has shown promising results. These data-driven approaches can help in the rapid and accurate extraction of material properties and transmission line parameters from measured or simulated data.
Nonlinear Kramers-Kronig Relations: The development of nonlinear Kramers-Kronig relations has extended the applicability of these relations to PCBs with nonlinear materials. These extended relations provide a framework for analyzing the nonlinear behavior of PCBs and predicting their performance under various operating conditions.

As the complexity of PCBs continues to increase and the demand for high-speed and high-frequency applications grows, the application of Kramers-Kronig relations in PCB analysis is expected to gain further importance. Future research directions may focus on the development of more advanced measurement techniques, the integration of Kramers-Kronig relations with multi-physics simulations, and the exploration of new materials and structures for PCBs.

Frequently Asked Questions (FAQ)

What are the Kramers-Kronig relations?
The Kramers-Kronig relations are a set of mathematical equations that describe the relationship between the real and imaginary parts of a complex function. They are based on the principle of causality and have found widespread applications in various fields, including the analysis of printed circuit boards (PCBs).
How are Kramers-Kronig relations used in PCB analysis?
Kramers-Kronig relations are used in PCB analysis to determine the dielectric constant and loss tangent of the materials used in the PCB. They also help in calculating the transmission line parameters, such as characteristic impedance and propagation constant, from measured or simulated scattering parameters (S-parameters).
What are the challenges in applying Kramers-Kronig relations to PCBs?
Some of the challenges in applying Kramers-Kronig relations to PCBs include the accuracy and bandwidth limitations of measurement techniques, numerical challenges in evaluating the integrals involved in the relations, and the presence of material nonlinearities. Researchers and engineers have been working on developing techniques to address these challenges.
What are some recent advancements in Kramers-Kronig-based PCB analysis?
Recent advancements in Kramers-Kronig-based PCB analysis include the development of broadband dielectric spectroscopy techniques, the integration of Kramers-Kronig relations with computational electromagnetics methods, the application of machine learning and data-driven approaches, and the development of nonlinear Kramers-Kronig relations for analyzing PCBs with nonlinear materials.
What are the future directions for research in this field?
Future research directions in the application of Kramers-Kronig relations to PCBs may focus on the development of more advanced measurement techniques, the integration of Kramers-Kronig relations with multi-physics simulations, and the exploration of new materials and structures for PCBs. As the complexity of PCBs continues to increase and the demand for high-speed and high-frequency applications grows, the importance of Kramers-Kronig relations in PCB analysis is expected to increase.

Conclusion

The Kramers-Kronig relations have proven to be a valuable tool in the analysis of printed circuit boards (PCBs). These relations, based on the principle of causality, provide a mathematical framework for relating the real and imaginary parts of complex functions, such as the dielectric constant and scattering parameters of PCBs.

The application of Kramers-Kronig relations to PCBs has enabled the determination of material properties, such as the dielectric constant and loss tangent, and the calculation of transmission line parameters, such as characteristic impedance and propagation constant. This information is crucial for understanding the electrical behavior of PCBs and optimizing their design for high-speed and high-frequency applications.

However, the application of Kramers-Kronig relations to PCBs is not without challenges. Limitations in measurement techniques, numerical challenges in evaluating the integrals, and the presence of material nonlinearities pose significant hurdles. Researchers and engineers have been working on developing advanced techniques and methodologies to overcome these challenges and improve the accuracy and practicality of Kramers-Kronig-based PCB analysis.

Recent advancements, such as broadband dielectric spectroscopy, computational electromagnetics, machine learning, and nonlinear Kramers-Kronig relations, have pushed the boundaries of what is possible in this field. As the complexity of PCBs continues to increase and the demand for high-performance electronic systems grows, the application of Kramers-Kronig relations in PCB analysis is expected to gain further importance.

Looking ahead, future research directions may focus on the development of even more advanced measurement techniques, the integration of Kramers-Kronig relations with multi-physics simulations, and the exploration of new materials and structures for PCBs. By pushing the frontiers of Kramers-Kronig-based PCB analysis, researchers and engineers can unlock new possibilities in the design and optimization of high-speed and high-frequency electronic systems.

In conclusion, the Kramers-Kronig relations have proven to be a powerful tool in the analysis of PCBs, enabling the determination of material properties and transmission line parameters. Despite the challenges and limitations, recent advancements and future research directions hold great promise for further enhancing the capabilities of Kramers-Kronig-based PCB analysis. As the field continues to evolve, the application of these relations will undoubtedly play a crucial role in shaping the future of high-performance electronic systems.