What is a Ripple Carry Adder?
A Ripple Carry Adder (RCA) is a digital circuit that performs the arithmetic operation of addition. It is one of the simplest and most fundamental building blocks in digital electronics. The RCA is constructed by cascading multiple full adders, where the carry output from each full adder is connected to the carry input of the next full adder in the chain.
The term “ripple carry” refers to the way the carry signal propagates through the adder. Starting from the least significant bit (LSB), the carry is generated and then “ripples” through the subsequent stages until it reaches the most significant bit (MSB). This sequential propagation of the carry signal is the main characteristic of the RCA.
How does a Ripple Carry Adder work?
To understand how a Ripple Carry Adder works, let’s first look at the basic building block: the full adder. A full adder is a digital circuit that takes three inputs (A, B, and Carry-in) and produces two outputs (Sum and Carry-out). The truth table for a full adder is as follows:
| A | B | Cin | Sum | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
The logic equations for the Sum and Carry-out outputs are:
Sum = A ⊕ B ⊕ Cin
Cout = (A · B) + (Cin · (A ⊕ B))
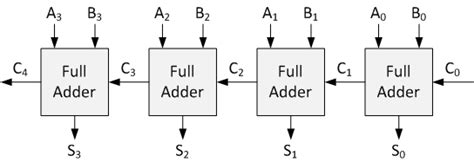
To create an n-bit Ripple Carry Adder, we connect n full adders in a chain. The Carry-out (Cout) from each full adder becomes the Carry-in (Cin) for the next full adder in the chain. The following diagram illustrates a 4-bit Ripple Carry Adder:
A3 B3 A2 B2 A1 B1 A0 B0
| | | | | | | |
v v v v v v v v
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
|FA3| |FA2| |FA1| |FA0| | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | |
| | | | | | | |
| +-------+ +-------+ +-------+ |
| |
+-----------------------------------------------+
|
v
Cout
In this example, A3-A0 and B3-B0 represent the two 4-bit numbers being added, and FA3-FA0 are the full adders. The Carry-out (Cout) from the most significant full adder (FA3) represents the overflow bit.
Advantages and Disadvantages of Ripple Carry Adders
Advantages:
1. Simple design and easy to understand
2. Requires fewer components compared to other adder architectures
3. Consumes less power due to its simple structure
4. Suitable for small-scale applications
Disadvantages:
1. Slow performance due to the sequential propagation of the carry signal
2. The delay increases linearly with the number of bits, making it unsuitable for high-speed applications
3. Not efficient for large-scale additions (e.g., 32-bit or 64-bit)
Alternatives to Ripple Carry Adders
Due to the limitations of Ripple Carry Adders, particularly their slow performance, several alternative adder architectures have been developed. Some of the most common alternatives include:
Carry Look-Ahead Adder (CLA)
The Carry Look-Ahead Adder (CLA) is designed to reduce the delay caused by the ripple carry effect. It calculates the carry signals in advance, based on the input signals, using additional logic. By generating the carry signals in parallel, the CLA can perform addition much faster than the RCA.
The CLA uses two additional terms: Propagate (P) and Generate (G). These terms are defined as follows:
Pi = Ai ⊕ Bi
Gi = Ai · Bi
The carry output for each stage can be expressed in terms of the Propagate and Generate terms:
Ci+1 = Gi + Pi · Ci
By calculating the carry signals in advance, the CLA can add numbers with a delay that is proportional to the logarithm of the number of bits, rather than linearly proportional as in the case of the RCA.
Carry Skip Adder (CSA)
The Carry Skip Adder (CSA) is another alternative to the RCA that aims to reduce the delay caused by the ripple carry effect. The CSA divides the adder into fixed-size blocks, each containing a Ripple Carry Adder. The carry-out from each block is generated by a separate circuit, which determines whether the block’s carry-in would propagate through to the next block.
If the carry-in does not affect the carry-out of a block, the carry-out is generated quickly, effectively “skipping” that block. This allows the CSA to achieve faster performance than the RCA, while still maintaining a relatively simple design.
Carry Select Adder (CSLA)
The Carry Select Adder (CSLA) is another adder architecture that aims to reduce the delay caused by the ripple carry effect. The CSLA divides the adder into multiple pairs of Ripple Carry Adders, each pair calculating the sum for a different carry-in value (0 and 1). A multiplexer then selects the correct sum based on the actual carry-in value.
By pre-calculating the sums for both possible carry-in values, the CSLA can reduce the delay caused by waiting for the carry to ripple through the adder. However, this comes at the cost of increased hardware complexity and power consumption compared to the RCA.
Applications of Ripple Carry Adders
Despite their limitations, Ripple Carry Adders still find use in various applications, particularly in small-scale digital systems where speed is not a critical factor. Some common applications include:
- Simple arithmetic logic units (ALUs) in microcontrollers and embedded systems
- Address calculation in memory systems
- Low-power, low-cost digital circuits
- Educational and training purposes to demonstrate the basics of digital addition

Implementing a Ripple Carry Adder
To implement a Ripple Carry Adder in a hardware description language (HDL) like Verilog or VHDL, you can create a module that instantiates multiple full adder modules and connects them in a chain. Here’s an example of a 4-bit Ripple Carry Adder implemented in Verilog:
module full_adder(
input A,
input B,
input Cin,
output Sum,
output Cout
);
assign Sum = A ^ B ^ Cin;
assign Cout = (A & B) | (Cin & (A ^ B));
endmodule
module ripple_carry_adder_4bit(
input [3:0] A,
input [3:0] B,
output [3:0] Sum,
output Cout
);
wire [2:0] carry;
full_adder FA0(
.A(A[0]),
.B(B[0]),
.Cin(1'b0),
.Sum(Sum[0]),
.Cout(carry[0])
);
full_adder FA1(
.A(A[1]),
.B(B[1]),
.Cin(carry[0]),
.Sum(Sum[1]),
.Cout(carry[1])
);
full_adder FA2(
.A(A[2]),
.B(B[2]),
.Cin(carry[1]),
.Sum(Sum[2]),
.Cout(carry[2])
);
full_adder FA3(
.A(A[3]),
.B(B[3]),
.Cin(carry[2]),
.Sum(Sum[3]),
.Cout(Cout)
);
endmodule
In this example, the full_adder module implements a single full adder, while the ripple_carry_adder_4bit module instantiates four full adders and connects them in a chain to create a 4-bit Ripple Carry Adder.
Conclusion
Ripple Carry Adders are a fundamental building block in digital electronics, providing a simple and straightforward way to perform binary addition. Although they have limitations in terms of speed and scalability, RCAs still find use in various small-scale applications and serve as an important educational tool for understanding the basics of digital addition.
As digital systems continue to evolve and demand higher performance, alternative adder architectures like Carry Look-Ahead Adders, Carry Skip Adders, and Carry Select Adders have been developed to address the limitations of RCAs. However, the simplicity and low power consumption of Ripple Carry Adders ensure that they will continue to have a place in the world of digital electronics.
Frequently Asked Questions (FAQ)
-
What is the main disadvantage of Ripple Carry Adders?
The main disadvantage of Ripple Carry Adders is their slow performance due to the sequential propagation of the carry signal. The delay increases linearly with the number of bits, making RCAs unsuitable for high-speed applications or large-scale additions. -
What is the difference between a half adder and a full adder?
A half adder is a digital circuit that can add two single-bit numbers, producing a sum and a carry-out. A full adder, on the other hand, can add three single-bit numbers (two operands and a carry-in), producing a sum and a carry-out. Full adders are the building blocks of Ripple Carry Adders, while half adders are used in the least significant bit position of an adder where there is no carry-in. -
What are some alternatives to Ripple Carry Adders?
Some common alternatives to Ripple Carry Adders include Carry Look-Ahead Adders (CLA), Carry Skip Adders (CSA), and Carry Select Adders (CSLA). These adder architectures are designed to reduce the delay caused by the ripple carry effect and improve the overall performance of the adder. -
Can Ripple Carry Adders be used for subtracting numbers?
Yes, Ripple Carry Adders can be used for subtracting numbers using the two’s complement method. To subtract a number B from A, you can add A to the two’s complement of B. The two’s complement of a number is obtained by inverting all the bits and adding 1 to the result. -
How do you implement a Ripple Carry Adder in a hardware description language (HDL)?
To implement a Ripple Carry Adder in an HDL like Verilog or VHDL, you can create a module that instantiates multiple full adder modules and connects them in a chain. The full adder modules perform the individual bit additions, while the connections between them propagate the carry signal from the least significant bit to the most significant bit.
No responses yet